볼린저 밴드와 통계학적 규칙

 

정규분포

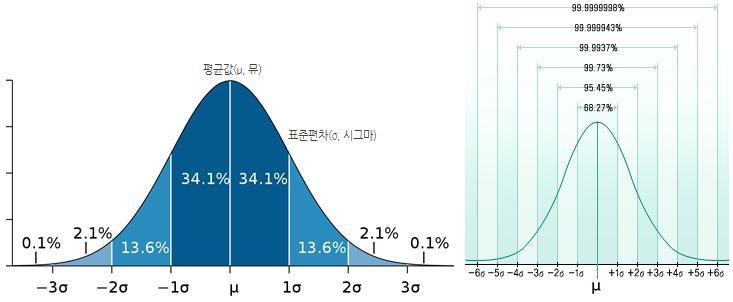
  평균에서 멀어지면 숫자는 적어진다. 이것이 정규분포 핵심입니다.

 

  이에 비해 주가의 변화로 똑같은 분포도를 만들어 보면 양 극단의 꼬리가 두껍게 나타납니다. 큰 폭의 이익과 큰폭의 손실이 예상보다 훨씬 많으며 소폭의 변화는 기대보다 훨씬 적습니다.

 

  즉 주가는 정규분포를 보이지 않으며 통계학적 규칙이 적용되지 않습니다.

 

  볼린저 밴드의 폭은 표준편차를 이용해 결정하므로 자연스럽게 통계학적 규칙을 따르게 됩니다. 주가는 비정규분포를 보이며 대개 표본 크기도 작지만 몇 가지 통계학적 개념은 유효합니다.

출처: https://drhongdatanote.tistory.com/57

  중심극한정리(Central limit theorem)는 주식의 경우처럼 데이터가 정규분포를 이루지 않을 때에도 표본값이 충분히 크다면 무작위로 표본을 추출했을 때 정규분포에 가까운 부분집합, 즉 통계학적 규칙이 유효한 집합을 얻을 수 있다는 이론입니다. 표본 크기가 비교적 작을 때 역시 모든 것이 완전히 들어 맞지는 않아도 통계학적 기대값이 어느 정도 유효하다는 것입니다.

출처:https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=businessinsight&logNo=221061151787 / 큰키가 우성이지만 평균회귀 원칙에 따라 전체 사람의 평균키는 무한정 커지지 않습니다.

  평균회귀(Regression to mean) 모든 것은 결국 평균값으로 돌아간다는 것을 뜻합니다. 주가도 평균에서 멀어지면 다시 평균으로 되돌아오리라 예측할 수 있는데, 이것이 기술적 용어인 과매수와 과매도의 기반이 되는 통계학적 개념입니다. 평균회귀를 주가에 적용하면 주가가 분포도의 끝쪽에 있을 때, 즉 볼린저 밴드의 상단이나 하단 가장자리에 있을 때 다시 평균, 즉 볼린저 밴드의 중앙으로 돌아갈 것임을 예측할 수 있습니다.

 

  기대한 만큼 높은 비율의 데이터, 즉 표준편차 밴드에 약 95%의 데이터가 포함되지 않는 이유는 두 가지로 요약할 수 있습니다.

 

  첫째, 우리가 이용하는 모집단 연산으로는 표본 연산보다 약간 좁은 밴드가 나옵니다.

 

  둘째, 주가가 정규분포를 이루지 않기 때문입니다. 주가는 양 극단에 훨씬 많이 분포하므로 밴드 바깥에 데이터가 더 많이 존재할 가능성이 높습니다.

 

  주가는 엄격한 의미의 사이클이 없고 사이클을 이용한 예측도 불가능하지만 변동성은 사이클을 보이며 사이클을 이용한 예측도 가능합니다. 따라서 주가는 사이클을 보이지 않아도 밴드는 이동평균에 대한 변동성을 반영하므로 밴드의 확장과 수축이 "일정한" 패턴을 보인다고 해서 별로 놀라운 사실은 아닙니다. 결국 낮은 변동성은 높은 변동성이 되고, 높은 변동성은 낮은 변동성이 되기 마련입니다.