<요약>
포트폴리오 분석은 포트폴리오로 알려진 투자 모음의 성과와 위험을 평가하는 과정이다. 포트폴리오 분석의 목표는 주어진 위험 수준에 대해 가장 높은 기대 수익을 제공할 최적의 투자 조합을 결정하는 것이다.
포트폴리오 분석에는 다음과 같은 몇 가지 방법이 사용된다:
1. Modern Portfolio Theory (MPT): 1950년대에 Harry Markowitz에 의해 개발된 MPT는 투자자들이 원하는 수준의 위험과 수익을 달성하기 위해 최적의 자산 조합을 식별하도록 돕는 수학적 프레임워크이다.
2. Capital Asset Pricing Model(CAPM): 윌리엄 샤프가 개발한 CAPM은 자산 포트폴리오에 대한 위험과 기대 수익 간의 관계를 설명하는 모델이다.
3. Black-Litterman Model: 투자자의 관점과 예측을 통합하는 포트폴리오 최적화 모델로, 주관적인 정보를 포트폴리오 최적화 프로세스에 통합할 수 있다.
4. Risk Parity: 기대 수익률에 관계없이 포트폴리오 내 다양한 자산의 위험 기여도 균형을 맞추는 것을 목표로 하는 포트폴리오 전략이다.
포트폴리오 분석 과정은 일반적으로 투자자의 목표와 제약을 파악하고, 포트폴리오의 현재 보유자산과 위험/수익 특성을 철저히 분석한 후, 포트폴리오의 전반적인 성과를 개선하기 위해 필요에 따라 조정하는 과정을 포함한다.
시장 상황, 경제 상황 및 개인 목표는 시간이 지남에 따라 변경될 수 있으므로 포트폴리오 분석은 지속적인 프로세스여야 한다.
7장은 포트폴리오 분석이다. 포트폴리오가 뭐냐~ 두개 또는 그 이상의 자산의 조합을 말한다. 즉 나눠서 투자하는 것을 뜻한다.
고등학교 때 다이어리처럼 썼던 프랭클린 포트폴리오와는 조금 개념이 다르다. (아 진짜 그거 도움 하나도 안돼. 괜히 비싸서 9천원이나 하고, 하여튼 포트폴리오만 들으면 그거 생각난다.)
예를 들어 보자,
| 비온다 1/2 | 맑다 1/2 | |
| 우산장사 | 100만 | 0 |
| 아이스크림 | 0 | 100 |
| 이익(예상 수익률) | 50 | 50 |
물론 맑을때도 나처럼 준비성 철저한 사람은 우산을 사둔다. 그리고 비와도 물론 더우면 아이스크림 먹는다. 하지만 여기서는 이러한 가정을 하겠다.
여튼 이러한 상황에서 각각 50% 분산 투자하면 어떻게 될까? 뻔하다, 분산이 0이 되면서 고정적으로 50만원의 수익을 얻을 수 있다.
σ^2= 1/2 * (50-50)^2 + 1/2 * (50-50)^2 = 0
이렇게 분산이 0이 됨을 보면서, 위험이 사라지는 것을 알 수 있다. 너무 쉽다고?
하지만 예제는 좀 더 복잡하다.
| 증권 | 투자비율 | 기대수익률 | 표준편차 | 공분산 |
| A | 70% | 10% | 20% | ρ= 0.5 (A,B의 공분산) |
| B | 30% | 20% | 30% |
틀리잖아! 해도 어쩔 수 없다. 현실성 없는 위의 예보다는 더 좋지 않는가?
이를 위해서는

이 식이 필요하다. 물론 그냥 하늘에서 떨어진 건 아니고, 다 나름의 구하는 과정이 있지만, 나와 이것을 볼 사람들에게는 무의미 하므로 생략하도록 하겠다. 혹시 더 궁금하다면...그냥 재무관리 책을 사시라.
하여튼 여기에 대입해서 풀어보자
잠깐 근데 σAB 값은 없지 않는가? 그것은 저번에 배운

이 식에서
유추할 수 있다.
다 대입해보면
(0.7^2)(0.2^)+(0.3^2)(0.3^2)+2*0.7*0.3*0.03
= 0.0403
이제는 투자 비율에 따른 포트폴리오를 한번 알아보자.
| 포트폴리오 | A | B | C | D | E |
| 투자비율 w1 | 1 | 0.7 | 0.4 | 0.3 | 0.0 |
| 투자비율 w2 | 0.0 | 0.3 | 0.6 | 0.7 | 1.0 |
| 기대수익률 | 20% | 18.5% | 17% | 16.5% | 15% |
| 표준편차 | 30% | 15% | 0% | 5% | 20% |

여튼 이를 통해 두 자산에 분배해서 투자하는 것이 활씬 위험이 적은 투자기회를 만들 수 있다는 것을 보여준다.
그런데 이 그림의 흥미로운 점은 자산 A와 자산 E 사이에 상관계수 ρ의 갚에 따라 무수히 많은 선들이 존제하는데 이 선은 포트폴리오의 위험의 변화를 나타낸다.

위의 곡선은 약 ρ가 0일때 곡선을 나타낸다. 상관관계가 음(-)일 수록 표준편차는 감소하며, 이는 위험감소효과가 커짐을 말한다.
그리고 이제
체계적 위험에 대해 알아보자, 이는 전반적인 경제환경의 변동에 따라 영향을 받는 위험을 말한다. 이것이 높으면 증권의 수익률이 시장전체의 변화에 민감하게 반응하는 것을 말한다. 대표적으로 금융주들이 되겠다.
그렇다면 당연히 비 체계적 위험이 있겠지. 인간은 이분하는걸 좋아하니까
이는 기업의 고유한 요인이나 그 기업이 속하여 있는 산업의 고유한 요인에 따라 결정되는 투자위험이다.
포트폴리오 내에 구성 증권의 수가 증가할 수록 비체계적 위험은 줄어들고 체계적 위험에 가까워진다.
이제 효율적 프론티어를 알아보자. 이는 나중에 8,9,10장까지 계속 다루게될 문제이다.
앞서 말한 포트폴리오를 통해 구성증권의 투자비율과 상관계수에 따라 하나의 곡선이 생긴다.

이것은 두개의 자산에대한 것이지만 만약 3, 4개라면 어떻게 될까?
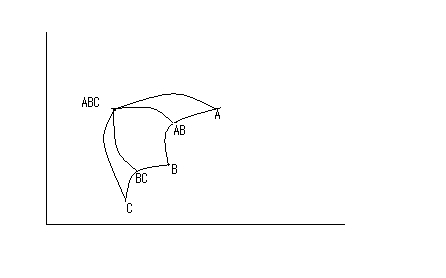
흠.... 조금 조잡하지만, 여튼 이런 모양이되고, A-ABC 곡선을 효율적 프론티어라고한다. 이는 다른 자산을 지배원리에 따라, 다른 자산은 선택하지 않고 이 자산을 최적배합으로 선택함을 말한다.
-다시 책을 베끼자면, 평균 분산 지배원리에 의해 선택된 포트폴리오를 효율적 포트폴리오라 하며 효율적 포트폴리오의 집합을 효율적 프론티어라고 한다.
최소분산 포트폴리오는 이 투자기회 집합의 기울기가 0이 되는 지점을 구하면 된다. 즉 분산을 w1(자산1)에 대해 편미분 하면 된다.
식으로 나타내면 다음과 같다. (미분 생략, 할 줄 알면 된다.)
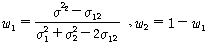
그리고 최적 포트폴리오를 구하는 것은, 개별 투자자의 효용곡선과 접하는 지점이다. 굳이 그림그리지 않아도 알겠지.
그리고 위험에 대해 보다 높은 기대수익률을 요구하는 놈일수록 보수적인 놈이다. 그 반대는 나같이 위험선호형
그리고 효율적 프론티어에 무위험 자산이 있을 경우 얘기가 약간 달라진다.
무위험 자산으로 예를 들자면 국공채가 있다. 예를들면 미국이 신용등급 AAA를 받어 가장 안전한 자산이란다.
여튼 무휘험 자산(1-w)와 위험자산 I 에 w를 투자하여 포트폴리오를 구성했을 때 기대수익률과 표준편차는 다음과 같다.
기대수익률 = (1-w)*Rf+w*E(Ri)
이때 Rf는 무위험 자산의 수익률이며, Ri는 위험자산의 수익률이다.
표준편차= (w^2 *σ^2*Ri)^1/2
= wσ(Ri)
'지식' 카테고리의 다른 글
| 투자론 - 선물 기본 (0) | 2020.11.02 |
|---|---|
| 노름꾼의 궤변 (0) | 2020.10.30 |
| 재무관리 6장 - 투자가치 측정 (0) | 2020.10.29 |
| 재무관리 5장 - 예제 및 연습문제 (0) | 2020.10.29 |
| 재무관리 5장 - 현금흐름 추정 (0) | 2020.10.28 |




댓글